Amplitude-Frequency Characteristics of the System “Mixing–Mixing” Heat Exchanger + Heat Transfer”
DOI:
https://doi.org/10.20535/1810-0546.2018.5.147067Keywords:
Mathematical modeling, “Mixing–mixing” heat exchanger, Performance indicator, Harmonic temperature fluctuations, Amplitude-frequency characteristicAbstract
Background. Mathematical modeling of continuous technological processes in non-stationary conditions caused by actions of various destabilizing factors is an actual problem. At the same time, analytical solutions have significant advantages over numerical ones, since they allow us to find out the nature of causation links in the analyzed properties of the modeling object and, as a practical result, to give physically well-founded recommendations for improving the efficiency of its functioning. The possible fluctuations in the temperature of heat carrier (HC) at the inputs of the flow heat exchanger (HE) cause instabilities for heat exchange processes. This usually leads to the efficiency decrease of the HE. Therefore, the calculation of its amplitude-frequency characteristics (AFC) has a significant (weighty) value.
Objective. The aim of the paper is to find out the behavior of the ideal “mixing–mixing” HE in stationary mode and harmonic fluctuations of temperature at the inputs of the apparatus and calculation of its AFC.
Methods. Known mathematical model in the form of a system of linear differential equations (reduced summed to dimensionless form) to calculate the effect of harmonic fluctuations of temperature on the stationary mode of the system “HE + heat transfer” was used.
Results. It is shown that the efficiency of the stationary mode of operation of the ideal “mixing – mixing” HE can be estimated by the efficiency indicator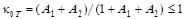 
, where 
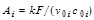– transfer number (k – heat transfer coefficient across the surface area F ; 
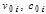– the volumetric flow rates of HC and their heat capacities). When 
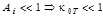, when 
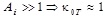(the process of heat transfer is much more intense compared with the process of heat outlet by flows from HE). AFC 
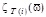of the system is calculated, where 
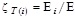– the simplex of the amplitudes of temperature fluctuations at the inputs and outputs; 
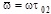– frequency complex (w – cyclic frequency, t02 – average time of stay of cold HC in HE).
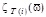are equal when the formal rearrangement of values Ai: 
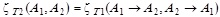, which is a reflection of the thermal “equality” of HC. When 
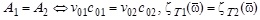; when 
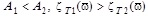at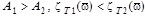 
. In the case 
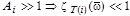(the intense heat transfer reduces the amplitudes of temperature fluctuations at the outputs of the HC). At relatively high frequencies, stationary mode is practically not violated at any values of Ai: 
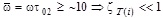. Therefore, in order to ensure practically stationary mode of HE operation, it is necessary to get rid of low 
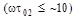harmonics of possible temperature fluctuations at the inputs.
References
W.M. Kays and A.L. London, Compact Heat Exchangers. Florida, Malabar: Krieger Publishing Company, 1998.
A.G. Bondar, Mathematical Modeling in Chemical Technology. Kyiv, Ukraine: Vyshcha Shkola, 1973.
H. Hausen, Heat Transfer in Countercurrent, Concurrent and Crosscurrent Flow. Heidelberg, Germany: Springer Verlag, 1976.
W.L. Luyben, Process Modeling, Simulation, and Control for Chemical Engineers. New York: McGraw-Hill, 1996.
J.M. Coulson and J.F. Richardson, Chemical Engineering, vol. 1, Fluid Flow, Heat Transfer and Mass Transfer. Oxford: Butterworth-Heinemann, 1999.
A.D. Polyanin et al., Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. London: Gordon and Breach Sci. Publ., 2002.
C. Boyadjiev, Theoretical Chemical Engineering. Modeling and Simulation. Berlin, Heidelberg, Germany: Springer-Verlag, 2010.
A.K Jana, Chemical Process Modelling and Computer Simulation. Delhi: PHI Learning Private Limited, 2011.
A. Rasmuson et al., Mathematical Modeling in Chemical Engineering. Cambridge: United Kingdom by MPG Print-group Ltd, 2014.
R. Serthn and T. Lestina, Process Heat Transfer. Principles and Applications. Cambridge, UK: Academic Press, Elsevier, 2014.
J.R. Welty et al., Fundamentals of Momentum, Heat, and Mass Transfer. New York: John Wiley & Sons Inc., 2014.
J.-P. Duroudier, Heat Transfer in the Chemical, Food and Pharmaceutical Industries. London, UK: ISTE Press, 2016.
I.D. Lucheyko and R.V. Kotsiurko, “Concurrent and countercurrent flow mode comparison in the tube in tube heat exchanger”, Naukovyi Ogliad, vol. 28, no. 7, pp. 15–26, 2016.
I.D. Lucheyko and R.V. Kotsiurko, “Efficiency coefficient of the “tube in tube” heat exchanger in the concurrent flow”, in Proc. XX Mendeleev Congress on General and Applied Chemistry, vol. 3, Yekaterinburg, Russia, 2016.
I.D. Lucheyko and R.V. Kotsiurko, “Temperature efficiency coefficient of the “tube in tube” heat exchanger in the countercurrent flow”, in Proc. XVІ Int. Sci. Conf. “High-Tech in Chemical Engineering–2016”, Moscow, Russia, 2016.
R.V. Kotsiurko and I.D. Lucheyko, “Mixing-mixing” heat exchanger as temperature signal transducer”, in Proc. VІ Int. Sci. Tech. Conf. “Current Issues in Modern Technologies”, Ternopil, Ukraine, 2017.
I.D. Lucheyko et al., “Frequency characteristics of a continuous stirred tank reactor at small perturbations of the concentration of a reagent (reaction )”, Visnyk TDTU im. I. Puliuja, vol. 11, no. 3, pp. 195–204, 2006.
Downloads
Published
Issue
Section
License
Copyright (c) 2018 Igor Sikorsky Kyiv Polytechnic Institute
This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under CC BY 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work
