The Convergence Rate in Precise Asymptotics for Series of Large Deviations
DOI:
https://doi.org/10.20535/1810-0546.2015.4.48791Keywords:
Precise asymptotics, Convergence rate, Series of large deviationsAbstract
Background. In the paper the sequence of independent identically distributed random variables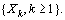 
is considered. We are interested in conditions for the convergence of series 
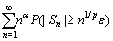for different values of parameters 
,
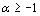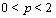and any 
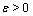. Such series appears while studying complete convergence as well as investigating various problems on large deviations in limit theorems of probability theory. The new approach to study such series is proposed by C. Heyde, who showed that if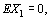 
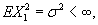then 
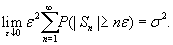Further, this result was extended by O. Klesov, and finally generalized by A. Gut, J. Steinebach and J. Hi for the series 
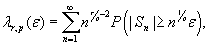with 
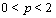, and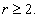 
.
Objective. We consider the series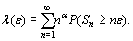 
for one-side deviations. The main purpose of the paper is to study precise asymptotics of function 
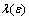while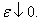 
Methods. The methods used to prove the main result is as follows: first we find the asymptotics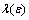 
for the partial case, i.e. we assume that random variables are Gaussian random variables, further we extend obtained result to the general case by means of estimations of rate of convergence in the Central limit theorem.
Results. In the paper the precise asymptotics of series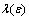 
while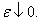 
for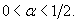 
is obtained. Strict assumptions imposed on parameter 
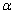are connected with the application of Nagaev inequality on the rate of convergence in the Central limit theorem.
Conclusions. The asymptotics 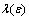ought to be considered for other values of 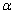as well. This requires though new techniques since the use of Nagaev inequality leads to some restrictions upon 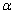. Since series 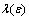converges (under some moment conditions) for any 
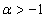then further investigations may concern the behavior of this series for 
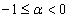and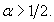 
References
P.L. Hsu and H. Robbins, “Complete convergence and the law of large numbers”, Proc. Nat. Acad. Sci.USA, vol. 33, pp. 25–31, 1947.
P. Erdös, “On a theorem of Hsu and Robbins”, Ann. Math. Statist., vol. 20, pp. 287–291, 1949.
F. Spitzer, “A combinatorial lemma and its application to probability theory”, Trans. Amer. Math. Soc., vol. 82, pp. 323–339, 1956.
M. Katz, “The probability in the tail of distribution”, Ann. Math. Statist., vol. 34, pp. 312–318, 1963.
L.E. Baum, M. Katz, “Convergence rates in the law of large numbers”, Trans. Amer. Math. Soc., vol. 120, pp. 108–123, 1965.
C.C. Heyde, “A supplement to the strong law of large numbers”, J. Appl. Probab., vol. 12, pp. 903–907, 1975.
O.I. Klesov, “On the convergence rate in a theorem of Heyde”, Theory Probab. Math. Stat., vol. 49, pp. 83–87, 1994.
A. Gut, J. Steinebach, “Precise asymptotics – a general approach”, Acta Math. Hung., vol. 138, pp. 365–385, 2013.
J. He, “A note to the convergence rates in precise asymptotics”, J. Inequalities Appl., vol. 378, 2013 [Online]. Avaliable: http://www.journalofinequalitiesandapplications.com/content/2013/1/378
S.V. Nagaev, “Some limit theorems for large deviations”, Teor. Veroyatnost. I Primenen., vol. 10, pp. 231–254, 1965.
Downloads
Published
Issue
Section
License
Copyright (c) 2017 NTUU KPI Authors who publish with this journal agree to the following terms:- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under CC BY 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work
