Investigation at the Extremum on the Average Time Delay of Packages of Self-Similar Traffic Described by the Weibull Distribution
DOI:
https://doi.org/10.20535/1810-0546.2018.5.146317Keywords:
Self-similar traffic, Queuing system, QoS characteristics, Weibull distribution, Packet delay timeAbstract
Background. The development of post-NGN networks leads to an increase in the range of high-speed services that require significant bandwidth and are sufficiently critical to time delays. This determines significant changes in the traffic structure and requires solving the problem of assessing the QoS characteristics when servicing traffic in the post-NGN network. It is possible to find the necessary amount of network resources to support them with the maximum and balanced load of network resources.
Objective. The aim of the paper is to investigate the extremum of some QoS characteristics of self-similar traffic, which is described by means of Weibull distribution.
Methods. Estimation of the average packet delay time of self-similar traffic for the queuing system QS 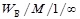 using the Weibull two-parameter distribution and the search for maximum and minimum of the average packet delay time were performed for different conditions of the queuing system operation and different values of packet service intensities and the Hurst parameter.
using the Weibull two-parameter distribution and the search for maximum and minimum of the average packet delay time were performed for different conditions of the queuing system operation and different values of packet service intensities and the Hurst parameter.
Results. Value for the average delay time of W packets in QS 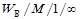 for different values of service rate packet
for different values of service rate packet 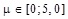 was defined, and dependence of the average waiting time of W packets in QS
was defined, and dependence of the average waiting time of W packets in QS 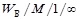 from the parameter a, which determines the shape of the Weibull distribution curve, was obtained. It is found that with increasing Hurst parameter, the average delay time value W of packets increases. It means that the increase of the high-speed services (Video Surviliance, smart-TV, HD-video) requires an increase in the size of the buffer devices to provide the required performance of network nodes of post-NGN network.
from the parameter a, which determines the shape of the Weibull distribution curve, was obtained. It is found that with increasing Hurst parameter, the average delay time value W of packets increases. It means that the increase of the high-speed services (Video Surviliance, smart-TV, HD-video) requires an increase in the size of the buffer devices to provide the required performance of network nodes of post-NGN network.
References
B.S. Goldstein, Communication Network Post-NGN, А.Е. Kucheryviy, Ed. St. Petersburg, Russia: BXV-Petersburg, 2014.
Networks of the Next Generation NGN, А.V. Roslyakov et al., eds. Moscow, Russia: Eko-Trends, 2008.
V.I. Tikhonov and P.P. Vorobiyenko, “Integrated telecommunication technology for the next generation networks”, in Proc. ITU Kaleidoscope: Building Sustainable Communities: Building Sustainable Communities, Kyoto, Japan, April 22–24, 2013, pp. 187–194. Available: https://ieeexplore.ieee.org/document/6533766
V.V. Кrylov and S.S. Samohvalova, Teletraffic Theory and Its Applications. St. Petersburg, Russia: BXV-Petersburg, 2005.
L.A. Fomin and G.I. Linets, “Taking into account the self-similarity properties of the load in network structures”, Proceedings of Tomsk Polytechnic University, vol. 33, no. 5, pp. 106–110, 2007.
О.I. Sheluhin and А.V. Оsin, “Influence of self-similarity of traffic on optimization of parameters of telecommunication networks”, Electrotechnical and Information Complexes and Systems, vol. 3, no. 1, pp. 55–59, 2007.
I.V. Strelkovskaya et al., “Self-similar traffic in G/M/1 queue defined by the Weibull distribution”, Radioelectronics and Communications Systems, vol. 61, no. 3, pp. 173–180, 2018. doi: 10.20535/S0021347018030056
I.V. Strelkovskaya et al., “Finding some QoS characteristics of self-similar traffic serviced by a mobile network”, in Proc. 2nd IEEE Int. Conf. Advanced Information and Communication Technologies-2017, Lviv, Ukraine, July 4–7, 2017, pp. 146–149. doi: 10.1109/AIACT.2017.8020086
L. Кleynrok, Theory of Queuing System Service, I.I. Grushko, Ed. Moscow, SU: Mashinostroyeniye, 1979.
G.M. Fikhtengolts, Fundamentals of Mathematical Analysis, vol. 2. Moscow, SU: Nauka, 1968.
Downloads
Published
Issue
Section
License
Copyright (c) 2018 Igor Sikorsky Kyiv Polytechnic Institute

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under CC BY 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work
