Two-Body Problem by the Singular Rank One Nonsymmetric Perturbation

Abstract

Background. We consider nonself-adjoint singular perturbation of rank one of a self-adjoint operator by nonsymmetrical potential, i.e., the formal expression \[\tilde{A}=A+\alpha \left \langle \cdot ,\omega _{1} \right \rangle\omega _{2},\] where A is semibounded self-adjoint operator in the separable Hilbert space  \[\mathfrak{H}, \alpha \in \mathbb{C}.\] In compare with many previous studies of self-adjoint perturbation, the vectors \[\omega _{1}, \omega _{2}\in \mathfrak{H_{-2}}\] are different, i.e., \[\omega _{1} \neq \omega _{2},\] that is some general problem about nonlocal interactions. The additional difficulties are that the Hilbert space H has a form of tensor product of spaces \[H=\mathfrak{K} \otimes \mathfrak{H},\] and the operator has a form \[\mathfrak{A}=\mathit{B}\otimes I_{\mathfrak{H}}+I_{\mathfrak{K}}\otimes \mathbf{\mathit{A}},\] which together illustrate the problem of two bodies.

Objective. The purpose of research in our work is the description of singular perturbation of operator of the form \[\mathfrak{\tilde{A}}=B\otimes I_{\mathfrak{N}}+I_{\mathfrak{K}}\otimes \tilde{A},\] where \[\tilde{A}\] is a self-adjoint operator that is singularly perturbed by nonsymmetric potential of rank one.

Methods. We use the assertion of about the presentation in the resolvent form of a rank one singular perturbation of a self-adjoint operator by symmetric potential, which corresponds to the problem of two bodies, and the definition of the operator singularly rank one perturbed by nonsymmetric potential \[\tilde{A}.\]

Results. The representation of the operator \[\mathfrak{\tilde{A}},\] given by formal expression in the form of resolvent is our main result.

Conclusions. We present the resolvent form for singularly perturbed self-adjoint rank one operator, which perturbed by nonsymmetric potential, appropriate the problem of two bodies. By representation we take into account the case when the perturbed operator requires additional parameterization. We look for the application of the general results to describe the problem with the use of two bodiesLaplace operator perturbed by nonsymmetric potentials composed of 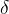-functions Dirac in  \[\mathbb{R}^{n}, n=2, 3.\]