Rank One Strong Singular Perturbation by Nonsymmetric Potential
DOI:
https://doi.org/10.20535/1810-0546.2014.4.28216Keywords:
Singular perturbation, Krein’s formula, Self-adjoint operator, Operator spectrumAbstract
For a rank one strong singular perturbation of a self-adjoint operator by nonsymmetric potential, we present a construction and investigated the corresponding eigenvalue problem. Namely we consider the perturbations of the form
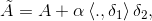
where A is a selfadjoint semi-bounded operator and
3.gif)
Such perturbation has an application in the theory of differential equations with retarded argument. The corresponding differential equations are the result of model control theory, particularly in electrical circuits. Examination conducted by methods of the theory of operators, including the application of the theory of extensions of densely defined symmetric operators to self-adjoint. Because the result is not self-adjoint operator, in considering building involved two symmetric operators, which is a narrowing of the original operator. This restrictions generated by different vectors of negative space
3.gif)
The presence of different vectors is the main difference between the proposed materials from previous studies in which perturbed operator was also self-adjoint. Also, the hallmark of previous publications is the fact that we consider a perturbation class .gif)
. In a previous publication perturbation class was considered .gif)
. The description problem is solved similarly to how the case was solved in a strictly singular perturbation symmetric potentials. Description is given by language of perturbed and unperturbed resolvents of operators, which are combined in a formula similar to Krein’s formula. Also in the paper we investigate the dot point, which appears by the operator .gif)
References
S. Albeverio and P. Kurasov, “Singular perturbations of differential operators. Solvable Schrödinger type operators”, in London Math. Soc. Lecture Note Series, Cambridge: Cambridge University Press, 2000, vol. 271, xiv+429 pp.
S. Albeverio et al., Solvable models in quantum mechanics, 2nd ed., AMS Chelsea Publishing,Providence,RI, 2005, xiv+488 pp.
Кошманенко В.Д., Дудкін М.Е. Метод оснащених просторів у теорії сингулярних збурень самоспряжених операторів. – К.: Ін-т математики НАНУ, 2013. – 320 c.
T. Kato and J.B. McLeod, “The functional-differential equation ”, Bull. Amer. Math. Soc., vol. 77, pp. 891–937, 1971.
V. Koshmanenko, Singular quadratic forms in perturbation theory (translated from the 1993 russian original by P.V. Malyshev and D.V. Malyshev), Mathematics and its Applications, vol. 474, pp. viii+308, 1999.
L.P. Nizhnik, “On rank one singular perturbations of selfadjoint operators”, Ibid, vol. 7, no. 3, pp. 54–66, 2001.
M.M. Malamud and V.I. Mogilevskii, “Kreĭn type formula for canonical resolvents of dual pairs of linear relations”, Methods Funct. Anal. Topology, vol. 8, no. 4, pp. 72–100, 2002.
T.V. Karataeva and V.D. Koshmanenko, “Generalized sum of operators”, Math. Notes, vol. 66, no. 5-6, pp. 556–564, 2000.
Downloads
Published
Issue
Section
License
Copyright (c) 2017 NTUU KPI Authors who publish with this journal agree to the following terms:- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under CC BY 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work
