Integral Transforms with the r-Hypergeometric Functions

Abstract

In the paper the r-hypergeometric function \[^{r}_{1}\Phi^{\tau ,\beta }_{1} (a;c;x)\] is considered in the form \[^{r}_{1}\Phi^{\tau ,\beta }_{1} (a;c;x)=\frac{1}{B(a,c-a)}\int t^{a-1}(1-t)^{c-a-1}e^{xt}{_1}\Phi^{\tau ,\beta }_{1}\left ( \alpha ;\gamma ; \frac{1}{t(1-t)}\right )dt,\] where \[^{r}_{1}\Phi^{\tau ,\beta }_{1} (a;c;x)=\frac{1}{B(a,c-a)}\int_{0}^{1}t^{a-1}(1-t)^{c-a-1}{_1}\Psi_{1}\begin{bmatrix} ^{(a,\tau);}_{(c,\beta);}& |xt^\tau \end{bmatrix}dt,\]  \[{_1}\Psi_{1}\left [ ... \right ]\] is the generalized Fox-Wright function. Its basic properties are investigated. The formulas of differentiation are valid: \[\frac{d}{dx}{_1^r}\Phi^{\tau ,\beta }_{1}(a,c,x)=\frac{a}{c}{_1^r}\Phi^{\tau ,\beta }_{1}(a+1;c+1;x),\frac{d^n}{dx^n\frac{}{}}{_1^r}\Phi^{\tau ,\beta }_{1}(a,c,x)=\frac{\Gamma (a)}{\Gamma (c)}\frac{\Gamma (a+n)}{\Gamma (c+n)}{_1^r}\Phi^{\tau ,\beta }_{1}(a+n;c+n;x).\] The generalized integralLaplace transforms

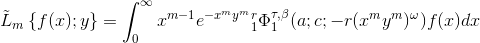
with function \[^{r}_{1}\Phi^{\tau ,\beta }_{1} (a;c;x) \] in the kernel are received. The main properties of these integral transforms are studied. The Parseval equality for the new generalized integral transforms are proved. The inverse formulas for these new integral transforms are received.