Contact Problem for Crank-Planetary Reduction Gear
DOI:
https://doi.org/10.20535/1810-0546.2018.1.121166Keywords:
Crank-planetary reducer, Contact problem, Design contact forceAbstract
Background. The problem of calculating the contact force in the parallelogram mechanism for taking the rotary motion from satellites in the crank-planetary gearbox, depending on the angle of rotation of the eccentric shaft of the gearbox, is considered.
Objective. The aim of the paper is to develop a method for calculating the contact force in the parallelogram mechanism, depending on the rotation angle of the gear unit eccentric shaft and determination of its maximum value. The maximum force value determines the maximum stresses of the mechanism parts, and, consequently, the strength of the gear unit as a whole.
Methods. In the first stage, on the basis of formulas of analytical geometry, the contact pairs of the parallelogram mechanism are classified on leading (active) and passive. In the second stage, the method of calculating the contact force in active contact pairs is given. This method is based on the principle of possible displacements in the framework of the assumption about the quasi-static operation mode of the crank-planetary reducer. When calculating the maximum stresses in contact pairs the classical formula for cylindrical surfaces can be applied.
Results. A formula is derived that allows you to set the numbers of leading contact pairs at a given position of the crank-planetary reducer's eccentric shaft. The resulting graph of the contact force in each contact pair is obtained. The formula for determining the approximate maximum value of the contact force in contact pairs is presented, which is valid for reducers with the number of such pairs from 3 to 10.
Conclusions. The results of the developed method of calculation of reducers with the parallelogram mechanism for taking the rotary motion from the satellites are presented. It was found out that when designing gears with a parallelogram mechanism for taking the rotary motion from satellites, the issues of ensuring the dynamic strength of its parts are relevant. When checking the contact strength or bending strength in the toothed engagement classical calculation methods can be applied. At the same time, when evaluating the strength of the satellite in the place of contact with the trickles of the reducer output link, Hertz’s formula can be applied, in which, as the design contact force, it should be taken to its maximum value, which is approximately equal to X×(4F/KN), where X = (0.8 + 0.05N)2 – K; F0 = T/L; T – torque at the output of the gear unit; KN – total number of contact pairs; L – The distance between the of the trickle axles and the gearbox axle. It should be noted that the above formula is obtained for reducers with K = 1; 2 and 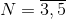 .
.
References
Planetary Gears, V.N. Kudryavtseva and Yu.N. Kirdyasheva, eds. Leningrad, SU: Mashinostroenie, 1977 (in Russian).
V.V. Kozyrev, Planetary Gearboxes as Part of Robots and Mechatronic Systems. Vladimir, Russia: Vladimir State University Publ., 2008 (in Russian).
I.I. Artobolevsky, Theory of Mechanisms and Machines. Moscow, SU: Nauka, 1988 (in Russian).
C. Jiankun, “Small tooth number difference planetary gear drive with a crank and oscillating block inputting mechanism”, Appl. Mech. Mater., vol. 52-54, pp. 1268–1273. 2011. doi: 10.4028/www.scientific.net/AMM.52-54.1268
S. Macovei and I. Doroftei, “An overview on internal geared mechanisms with small difference between teeth number”, IOP Conf. Ser.: Mater Sci. Eng, vol. 95, p. 012053, 2015. doi: 10.1088/1757-899X/95/1/012053
T.I. Plekhanov, “Structures and strength properties of planetary gear with internal linkings wheel strength”, East. Eur. Sci. J., iss. 1, pp. 144–156, 2014. doi: 10.12851/EESJ201402ART28
G.A. Timofeev et al., “Сrank-planetary reduction reducers with involute internal gearing with the difference of the number of teeth Zd = 1”, Konversija v Mashinostroenii, no. 3, pp. 43–45, 2004 (in Russian).
O.E. Pechkovskaya et al., “Modification of the internal involute gear with a small difference in the number of teeth of the wheels”, Bulletin of the Belarusian-Russian University, no. 1, pp. 91–98, 2012 (in Russian).
F.I. Plekhanov and S.M. Molchanov, “Problems of designing a high-loaded planetary gear with a roller movement removal mechanism”, Bulletin of the Kazan State Technical University named after. A.N. Tupolev, no. 3, pp. 64–67, 2012 (in Russian).
X.N. Feng, “Research on stress characteristics of planetary gear drive with small tooth number difference”, in Proc. 3rd Int. Conf. Mech. Eng. Intell. Syst., 2015, pp. 433–438. doi: 10.2991/icmeis-15.2015.80
I.A. Birger et al., Calculation of the Strength of Machine Parts. Moscow, Russia: Mashinostroenie, 1993 (in Russian).
Downloads
Published
Issue
Section
License
Copyright (c) 2018 Igor Sikorsky Kyiv Polytechnic Institute

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under CC BY 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work
